This is a follow up article to my previous article explaining why I prefer ranked choice voting over approval voting. The task here is to explain why I prefer ranked choice voting (RCV) over Condorcet for most elections.
To not keep you in suspense, I’ll tell you up front. It is MUCH harder for voters to understand how Condorcet ballots are counted than to understand how RCV ballots are counted. In my view, it is very important for voters to understand the counting process. For this reason, I recommend that most organizations use RCV and not Condorcet.
With both RCV and Condorcet, voters cast the same exact ranked ballot. The difference is how the ballots are counted to determine the winner, and I’ll explain this next.
Counting RCV Ballots
With RCV, the ballots are counted in rounds, and here is an example of RCV results. For the first round, each ballot is allocated to its first choice. For each subsequent round, the last-place candidate is eliminated, and the ballots of the last-place candidate are transferred to the next choices on the ballots. The counting is complete when a candidate has a majority or only two candidates remain.
Counting Condorcet Ballots
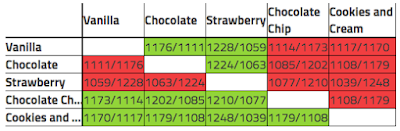
With Condorcet, the ballots are counted for each possible pair of candidates. Here is an example of Condorcet results, and I’ve copied the table into this post.
For the 5 candidates in the this poll, there are 10 possible pairs of candidates (Choc/Van, Straw/Van, Straw/Choc, CChip/Van, CChip/Choc, CChip/Straw, C&C/Van, C&C/Choc, C&C/Straw, and C&C/CChip).
Each cell of the table tells you who would win a pairwise contest between the candidate on the row and the candidate on the column. The diagonal of the table is empty since it doesn’t make sense to compare a candidate to him or herself.
Consider the first row (the Vanilla row). The second cell indicates that Vanilla beat Chocolate by 1176 to 1111. This means that of the 2287 ballots, 1176 of them ranked Vanilla higher than Chocolate and 1111 ranked Chocolate higher than Vanilla. Accordingly, if only these two candidates were competing in the election, then Vanilla would be the winner.
Continuing with the first row, you can see that Vanilla beats Strawberry but both Chocolate Chip and C&C beat Vanilla. You can continue with the other rows to see which candidates win all of the pairwise elections. Note that the table is symmetric about the diagonal since Vanilla beating Chocolate (first row second cell) requires that Chocolate lose to Vanilla (second row first cell).
Looking at the entire table, we see that C&C beats every single one of the other candidates in pairwise elections, and accordingly C&C is the winner.
This isn’t, however, the end of the story… It is possible that no one candidate beats all of the other candidates. For example, it is possible that C&C beats everyone except Vanilla, and that Chocolate beats Vanilla. In this situation we have:
- C&C > Chocolate > Vanilla (C&C beats Chocolate and Chocolate beats Vanilla)
- C&C < Vanilla (C&C loses to Vanilla)
Applying the transitive property that you all remember from high school geometry, we have a contradiction. C&C is both greater than (#1) and less than (#2) Vanilla. This is called a Condorcet cycle and you can think of it as a paradox of the beliefs of the voters.
When a Condorcet cycle happens, you need another way of choosing the winner. I personally like to think of the Condorcet cycle as a tie, and you need to break the tie. For example, you could use RCV to break the tie.
Most Organizations Should Use RCV
Above, it took one paragraph to explain counting RCV ballots and ten paragraphs to explain counting Condorcet ballots. It is going to be much harder for voters to understand how Condorcet ballots are counted than to understand how RCV ballots are counted.
For this reason, I recommend that most organizations use RCV instead of Condorcet. The voters will want to understand how the winner was determined (especially in a close and/or contentious election), and this is a much more straightforward task for RCV.
This is a soft science conclusion, and others will certainly disagree. One could also make the argument that we should use the plurality method instead of RCV because the plurality method is easier to understand than RCV. I disagree with that argument, but you can’t say that it is “wrong” or “right”.
For me, RCV hits the sweet spot of providing good election outcomes but also making it easy for voters to understand how votes are counted.
Although…
Despite the above, Condorcet is actually a better method of counting ballots than ranked choice voting in a pure mathematical sense (e.g., not factoring in other factors such as voter understandability). It is possible that a candidate will beat all other candidates in pairwise elections but not win an ranked choice voting election. Although this is relatively rare, in such a situation, Condorcet elects a “better” candidate than ranked choice voting and it is hard to argue otherwise.
Accordingly, where the voters are more sophisticated mathematically (e.g., electing the president of the math team), then I recommend that the organization use Condorcet voting instead of ranked choice voting.