Making the switch to online voting can prompt some understandable concerns. Voters who are used to physical ballots may wonder what happens to votes that are collected and tallied with the help of online voting software. But as the advantages of online voting tools quickly reveal themselves, your voters will love online voting as much as we do.

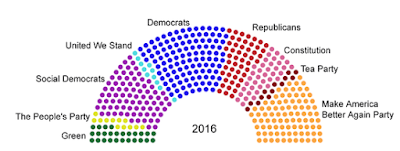When electing a group of people, such as a congress, council, or committee, you need to decide which philosophy of representation that you would like to use. At a very high level, there are two basic options: proportional representation or majoritarian representation.

Brian Meek

Meek STV is the creme de la creme of STV counting rules. For you math nerds, I would even call it a beautiful algorithm! To appreciate all that beauty, we’re going to have to get our hands dirty. I’m going to assume that you have a solid understanding of STV and that you’ve read our previous post describing Scottish STV. Feel free to brush up on STV and come back later if you need to.

When organizations introduce online voting or make the switch to an online voting service, their voting members naturally voice their concerns about the change. These concerns stem from the need to have accessible, accurate, and secure voting processes for every voter. For those organizing the election, reliable results are crucial to maintaining confidence in the organization’s governance. When weighing your options for voting systems, you may encounter the following questions.

“My scheme is intended only for honest men.”

The Borda count is a great voting system that doesn’t get enough attention. It is really easy to understand and is very useful for certain types of elections. It does, however, have a serious flaw that you need to be aware of before using it. More on that later.

This is a follow up article to my previous article explaining why I prefer ranked choice voting over approval voting. The task here is to explain why I prefer ranked choice voting (RCV) over Condorcet for most elections.

Whether it’s to decide the flavor of ice cream to serve at the church social or decisions of international import, election time is always exciting! Seeing people line up for the polls or eagerly awaiting ballots by mail, counting the votes and finally announcing the winners. But elections are also nerve-wracking for those who run them. Keeping track of the ballots, ensuring voters have access to information, and keeping returned ballots safe until counting makes voting day a long one for election staff. If your organization has a small staff, OpaVote’s voting software make voting day a breeze while losing none of the excitement.