There are two points to showing this example.
First, the title relates to Arrow's Theorem, which loosely speaking, proves that all methods of counting votes are flawed in some way. It sounds fatalistic at first. How can we possibly elect our leaders if there is no right way of doing so?
Well, no voting system is perfect, but many of them are good. There are lot's of differences of opinion as to which voting system is "best" or should be used for different applications. Your organization needs to consider the options and select what you think is best (we have recommendations here, here, here, and here).
Second, your organization needs to be clear in stating which voting system will be used. Different voting systems can produce different results and you don't want a post election dispute over who the winners are! Even smaller changes to counting rules can affect the outcome so a good way to be precise is to state that San Francisco RCV or Scottish STV will be used (both of which are implemented by OpaVote).
Now let's get to the example that causes three different winners under plurality, IRV, and Condorcet. Note that, most of the time, most voting systems produce the same results so that this is definitely a contrived example.
Ballots
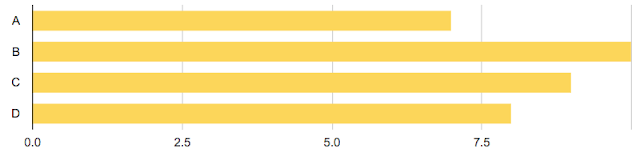
We have 34 ballots with 4 candidates who we will call A, B, C, and D. Here are the ballots:- 10 voters rank B first, A second, C third, and D fourth
- 9 voters rank C first, A second, B third, and D fourth
- 8 voters ranks D first, A second, C third, and B fourth
- 7 voters rank A first, C second, D third, and B fourth
Plurality Voting
Plurality voting is really easy. Candidate B has the most first place votes and is thus the plurality winner.
Instant Runoff Voting
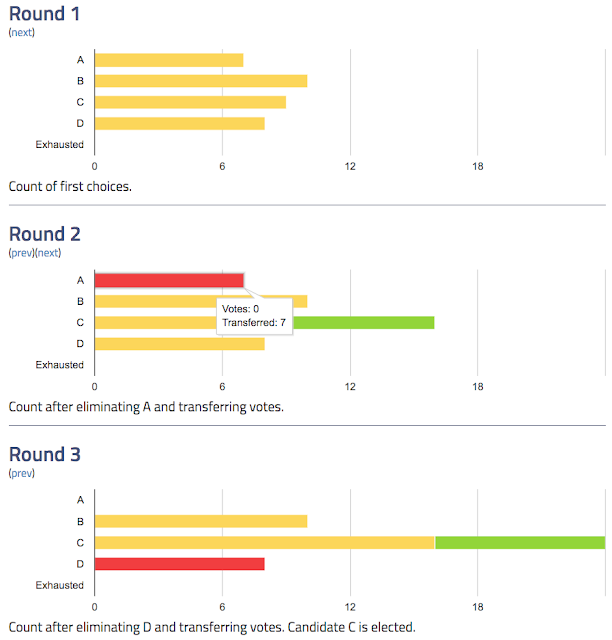
With IRV, we eliminate the last place candidate and transfer votes until we have a winner. As you can see below, Candidate A has the fewest votes at round 1, and Candidate D has the fewest votes at round 2. In round 3, Candidate C has a majority and is the IRV winner.
The plurality winner, Candidate B, doesn't win under IRV because Candidate B is not popular among supporters of the other candidates. In fact, Candidate B wasn't anyone's second choice!
Condorcet Voting
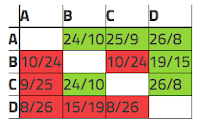
Condorcet voting is a little harder to explain and visualize. With Condorcet, the winner of the election is the candidate who wins all pairwise elections (if such candidate exists). The table below illustrates this.
The first row indicates that Candidate A beats Candidate B by 24 to 10, Candidate A beats Candidate C by 25 to 9, and Candidate A beats Candidate D by 26 to 8. Since Candidate A beats all of the other candidates in pairwise elections, Candidate A is the Condorcet winner. Similarly, the other rows show how the other candidates fared in pairwise elections (B loses to A and C but beats D, C loses to A but beats B and D, and D loses to everyone).
The plurality winner, Candidate B, did not do well with Condorcet since he lost to both Candidate A and Candidate C.
The IRV winner, Candidate C, lost to Candidate A because Candidate A was a very popular second choice. Although Candidate A had the fewest first choices, Candidate A was second on every other ballot. Proponents of Condorcet voting often cite this as a benefit over other voting systems, and see here for a more in-depth comparison.
